Proprietà colligative delle soluzioni:
– innalzamento ebullioscopico
– abbassamento crioscopico
– pressione osmotica e abbassamento della tensione di vapore (che non esamineremo in questo post)
Semplificando: un soluto non volatile aggiunto ad un solvente cambia le proprietà chimico-fisiche della soluzione che ne deriva.
Facciamo un esempio pratico: quando cuociamo la pasta, aggiungendo il sale all’acqua, cambiamo il punto di ebollizione dell’acqua pura. I 100 °C non basteranno, ne serviranno un po’ di più. La stessa soluzione (acqua+sale) messa in freezer non congelerà a 0 °C come l’acqua pura ma ad una temperatura che può arrivare diversi gradi sotto lo zero (abbassamento crioscopico)
L’entità del cambiamento dipende essenzialmente dalla concentrazione del soluto (sale, zucchero, ecc..) che la soluzione contiene.
Uno sciroppo molto zuccherino, come può essere ad esempio il miele, non congelerà a 0 °C, ma a temperature nettamente inferiori. Questo perché la concentrazione di zucchero è tale da impedire all’acqua presente di essere libera di congelare alla temperatura alla quale congelerebbe se fosse pura. Estremizzando, lo zucchero puro non congela nemmeno a – 40 °C.
Del resto, già Galileo Galilei con il suo termometro ad alcol, all’inizio del 1600 aveva notato che 2 parti di ghiaccio + 1 parte di sale (NaCl, cloruro di sodio) abbassavano la temperatura a -20 °C prima che questa soluzione congelasse.
Prendendo in considerazione ciò che si applica al gelato, l’equazione espressa sopra è quella che regola l’abbassamento del punto di congelamento. Infatti anche grazie agli zuccheri (soluti) presenti nella miscela si può ottenere un gelato morbido alle usuali temperature di servizio (mediamente il range va dai -6 °C ai – 14 °C).
Cosa dice l’equazione?
∆Tc = Kc* b
∆Tc = abbassamento crioscopico (°C)
Kc = costante crioscopica molale (per l’acqua: 1,86 °C*kg/mol)
b = molalità (mol soluto/kg solvente)
Più soluto (sali, zuccheri, …) si aggiunge od è presente in un liquido (acqua, latte, succo,..) minore sarà la temperatura a cui l’acqua disponibile congelerà.
Unendo questa informazione a quelle derivanti dal potere dolcificante e dalla resistenza al congelamento si può iniziare ad avere una visione allargata di quello che accade in sistema complesso come il gelato.
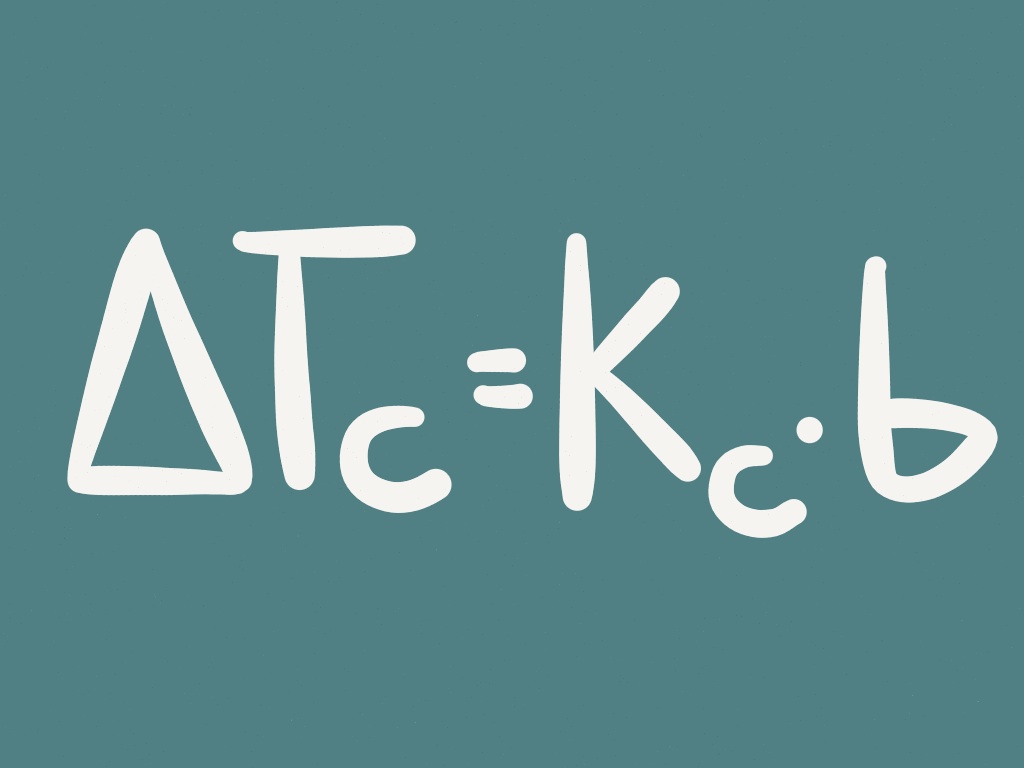




[…] 4 il ghiaccio continua a formarsi, i cristalli si strutturano. Come spiegato in un precedente post, i soluti a basse temperature tendono, per effetto del congelamento del solvente acqua, a […]
[…] che viene servito a temperature intorno ai -10/-12 °C, questo prodotto trova il suo optimum di servizio a temperature più alte (tra i 0°C/-4°C fino a +8/+10 […]
[…] durante e alla fine del processo di congelamento, una parte di acqua non congelata è sempre […]
[…] scientifici, tradizionali giusto per citarne […]
[…] bollente per mantenerne poi il colore brillante. Una curiosità: anche se può sembrare strano, il congelamento, in certi casi, porta ad aumentare il numero delle reazioni enzimatiche così come la velocità […]
[…] ed altre approssimazioni, fare delle previsioni relative all’attività dell’acqua di sistemi alimentari più complessi che comunque, soprattutto nello sviluppo di nuovi alimenti, è indispensabile […]
[…] ad uno snack freddo, tipo gelato o semifreddo e non avendo a disposizione una gelatiera abbiamo tentato di crearne uno che potesse […]
Ma nella relazione di abbassamento crioscopico non hai considerato il coefficiente di van’t hoff, per cui la relazione va bene per 1 o 2 soluti, ma non ha soluzioni per più di 2 soluti o per soluti di cui non si conosce il coefficiente.
[…] -Abbassamento crioscopico, Food in Progress, 2013, https://www.foodinprogress.com/abbassamento-crioscopico/ […]